Método de reducción
Concepto: consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita.
Pasos del método de reducción
Para resolver un sistema de ecuaciones por el método de reducción seguiremos los siguientes pasos:
1 Se preparan las dos ecuaciones, multiplicándolas por un numero tal que las ecuaciones resultantes tengan un coeficiente en común
2 Realizamos una resta (o suma según sea el caso de los signos de los coeficientes) para desaparecer (eliminar) una de las incógnitas
3 Se resuelve la ecuación resultante
4 El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve
5 Los dos valores obtenidos constituyen la solución del sistema
Veamos un ejemplo:
1. Escogemos una incógnita a eliminar: la y.
2. Sus coeficientes son -1 en la primera ecuación y 1 en la segunda. Como son iguales y de signo contrario, sumaremos las ecuaciones para que desaparezca la incógnita.
3. Sumamos las ecuaciones para eliminar la y:
4. Resolvemos la ecuación obtenida:
5. Calculamos la otra incógnita sustituyendo: sustituimos la incógnita x por 7 en alguna de las ecuaciones y la resolvemos:
La solución del sistema es
Nota: si ninguna de las incógnitas tiene el mismo coeficiente, podemos multiplicar cada ecuación por el número distinto de 0 que sea necesario para conseguirlo.
Aquí podemos observar un video de apoyo:
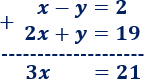
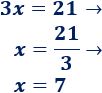
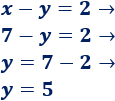

No hay comentarios:
Publicar un comentario