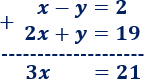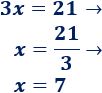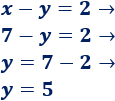Reciban un cordial saludo de mi parte Marco Sánchez
Les vengo a invitar a que puedan aprender y saber más de matemáticas básicas y todo en general
Lo tema del día que les mostrare y les ayudare es de los sistemas de ecuaciones por sus metodos de igualación, sustitución. reducción y método de cramer
Para esto necesitaremos que te pongas comodo y des el mayor esfuerzo de ti para poderte ayudar y que puedas mejorar en tus estudios y salir adelante en lo que te gusta, conllevando las matemáticas
Proyecto de matematica
Blog matemático que te ayudara a poder salir adelante con nuestra ayuda y tu mente.
sábado, 16 de enero de 2021
Saludos
jueves, 14 de enero de 2021
Sistemas de ecuaciones
Sistema de ecuaciones
Concepto: En matemáticas, un sistema de ecuaciones algebraicas es un conjunto de ecuaciones con más de una incógnita que conforman un problema matemático que consiste en encontrar los valores de las incógnitas que satisfacen dichas operaciones.
Objetivo: El propósito fundamental de las ecuaciones lineales es el de establecer un método para obtener soluciones a los problemas prácticos que con frecuencia aparecen en casi todos los campos de estudio, es decir, representarlos mediante modelos matemáticos.
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común.
En esta ocasión vamos a resolver un sistema de 1 ecuaciones lineales con 3 incógnitas.
Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas.
Una solución es todo par de números que cumple la ecuación.
Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones:
- Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto.
- Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden.
- Incompatible: No tiene solución, la representación son dos rectas paralelas.
Existen diferentes métodos de resolución:
- Sustitución.
- Reducción.
- Igualación.
- Cramer
Método De Sustitución
Método de sustitución
- Despejar una de las incógnitas de una ecuación y sustituir la expresión resultante en la otra, que se transforma en una ecuación lineal con una incógnita.
- Despejar la incógnita de dicha ecuación lineal y sustituir su valor en la ecuación inicial para hallar el valor de la otra incógnita.
Para resolver un sistema de ecuaciones por el método de sustitución seguiremos los siguientes pasos:
1 Se despeja una incógnita en una de las ecuaciones
2 Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita
3 Se resuelve la ecuación
4 El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada
5 Los dos valores obtenidos constituyen la solución del sistema
También hay que tener en cuenta que para plantear un sistema de ecuaciones, sobre todo si se pretende que los resultados sean valores enteros, lo mejor es partir de valores conocidos para las incógnitas y plantear ecuaciones en las que las igualdades sean ciertas.
Método de igualación
Método de Igualación
¿Qué es el método de igualación?
Tal como sugerimos anteriormente, el método de igualación es una técnica perteneciente al mundo de las Matemáticas. Se trata de una ligera variante del conocido método de sustitución (que puedes conocer a fondo ingresando en este artículo de nuestra autoría). Como seguramente habrás podido apreciar, tras la sucesiva lectura de distintos artículos, no hay una única vía para resolver problemas de corte matemático. Dado que hay ecuaciones o expresiones de distinta complejidad y características, es posible abordar un método u otro según el caso.
De cualquier manera, la técnica de la que estamos hablando sirve para encontrar el resultado de un sistema de ecuaciones; y básicamente se aplica despejando la misma incógnita en ambas expresiones y luego igualando el resultado de los dos procedimientos de despeje. De esta forma, consigues una ecuación de grado 1 (primer grado) que consiste en la respuesta al sistema completo.
En palabras más sencillas, el método de igualación implica despejar 1 de las incógnitas (siempre la misma) de ambas ecuaciones y a continuación, igualar los dos resultados. Así, obtienes un único sistema de 1 ecuación con 1 incógnita. Seguidamente, tienes que repetir el mismo procedimiento con la incógnita restante. Es muy probable que ya hayas oído explicar esta técnica a algún profesor de la escuela, porque debido a que resulta muy simple y básica, es una de las que primero se enseñan antes de pasar a desafíos matemáticos más complejos.
Es importante tener en cuenta que el método de igualación suele utilizarse únicamente siempre que ha sido despejada exactamente la misma incógnita por medios distintos. De lo contrario, los expertos recomiendan recurrir a otras opciones como por ejemplo el método de sustitución o el método de Gauss. Esto es así porque, por lo general, tal método no es capaz de solucionar problemas más complejos que trasciendan el tema de las ecuaciones lineales con 2 incógnitas.
Pasos del método de igualación
No serviría de nada que te explicáramos la definición de “método de igualación” si no fuéramos capaces de mostrarse cómo se aplica en la práctica. A continuación damos un paso a paso bien detallado de lo que tienes que hacer para llegar a resolver el problema matemático que te ocupa.
- Detectar la incógnita y despejarla en las 2 ecuaciones que conforman el sistema.
- Igualar las expresiones resultantes.
- Resolver la ecuación lineal con 1 incógnita, resultado del paso anterior.
- Calcular el valor de la incógnita restante, reemplazando la encontrada en 1 de las ecuaciones despejadas del primer paso.
Método de Reducción
Método de reducción
Concepto: consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita.
Pasos del método de reducción
Para resolver un sistema de ecuaciones por el método de reducción seguiremos los siguientes pasos:
1 Se preparan las dos ecuaciones, multiplicándolas por un numero tal que las ecuaciones resultantes tengan un coeficiente en común
2 Realizamos una resta (o suma según sea el caso de los signos de los coeficientes) para desaparecer (eliminar) una de las incógnitas
3 Se resuelve la ecuación resultante
4 El valor obtenido se sustituye en una de las ecuaciones iniciales y se resuelve
5 Los dos valores obtenidos constituyen la solución del sistema
Veamos un ejemplo:
1. Escogemos una incógnita a eliminar: la y.
2. Sus coeficientes son -1 en la primera ecuación y 1 en la segunda. Como son iguales y de signo contrario, sumaremos las ecuaciones para que desaparezca la incógnita.
3. Sumamos las ecuaciones para eliminar la y:
4. Resolvemos la ecuación obtenida:
5. Calculamos la otra incógnita sustituyendo: sustituimos la incógnita x por 7 en alguna de las ecuaciones y la resolvemos:
La solución del sistema es
Nota: si ninguna de las incógnitas tiene el mismo coeficiente, podemos multiplicar cada ecuación por el número distinto de 0 que sea necesario para conseguirlo.
Aquí podemos observar un video de apoyo:
Método de Cramer
Método de Cramer
Resolver un sistema de ecuaciones lineales es a priori complicado, aunque se dispone de métodos para atacar dichos problemas.
Existe por ejemplo el método de Gauss, pero ahora vamos a ver la regla o método de Cramer.
Dicha regla sólo puede utilizarse si el sistema de ecuaciones que se pretende resolver cumple dos condiciones:
- El sistema tiene el mismo número de incógnitas que de ecuaciones.
- El determinante de la matriz de los coeficientes es diferente de cero.
CONDICIONES
Para poder aplicar este método se deben cumplir las siguientes condiciones:
- El número de ecuaciones debe ser igual número de incógnitas, es decir, si tenemos dos variables, debemos tener dos ecuaciones.
- El determinante de la matriz de los coeficientes debe ser distinto de cero.
- Las ecuaciones deben estar preparadas, de tal manera que las incógnitas queden en columnas a la izquierda del signo igual y los términos independiente a la derecha.
Aquí tenemos un video de apoyo:
Saludos
Reciban un cordial saludo de mi parte Marco Sánchez Les vengo a invitar a que puedan aprender y saber más de matemáticas básicas y todo en ...

-
Método de sustitución Concepto: consiste en despejar o aislar una de las incógnitas (por ejemplo, x x ) y sustituir su expresión en la o...
-
Método de Cramer Método de Cramer concepto: Regla de Cramer . Un sistema de ecuaciones lineales recibe el nombre de sistema de Cramer cu...
-
Método de Igualación Concepto: El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones y después igualar lo...